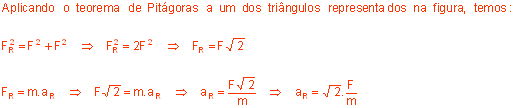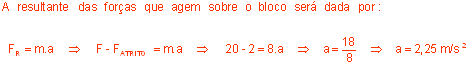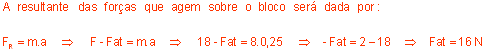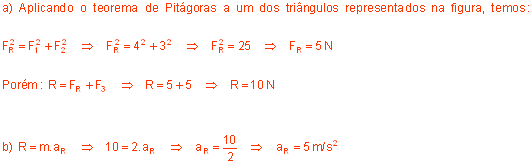1. (FATEC-SP) - Uma partícula de massa m é submetida simultaneamente e exclusivamente à ação de duas forças constantes perpendiculares e de mesma intensidade F. Calcule a aceleração da partícula.
2. (VUNESP) - A força de intensidade F atuando isoladamente no corpo de massa m produz uma aceleração resultante de módulo a. Se duas forças perpendiculares atuarem no corpo de massa m, conforme ilustra a figura, qual será a intensidade da aceleração resultante aR ?
3. (UNITAU) - Duas forças de 20 N cada uma atuam simultaneamente sobre uma partícula de massa 2,0 kg. Sabendo que as forças têm direção que formam ângulo de 120o, determinar:
a) a aceleração da partícula;
b) o ângulo formado entre a aceleração da partícula e uma das forças.
4. (FAAP-SP) - Um bloco de massa 8,0 kg é puxado por uma força de 20 N como mostrado na figura. Sabendo-se que a força de atrito entre o bloco e a superfície é de 2,0 N calcule a aceleração a que fica sujeito o bloco em m/s2.
5. (MED. ITAJUBÁ) - O bloco B, da figura abaixo, possui massa igual a 8,0 kg e está em movimento retilíneo sobre uma mesa plana e horizontal. A força, constante e de módulo igual a 18 N, aplicada sobre o bloco, é responsável pelo seu tipo de movimento. Sabendo-se que a aceleração do bloco é também constante, e vale 0,25 m/s2, qual será o valor da força de atrito entre o bloco e a mesa, medida em unidades SI?
6. (ENG. ALFENAS) - Sobre um livro de massa 2,0 kg atuam apenas três forças constantes: F1 = 4,0 N; F2 = 3,0 N e F3 = 5,0 N conforme o esquema a seguir, onde F1 e F2 são perpendiculares.
Calcule:
a) O módulo da força resultante sobre o livro.
b) O módulo da aceleração adquirida pelo livro.
7. (FATEC-SP) - Um bloco está apoiado sobre uma superfície horizontal sem atrito e, inicialmente, em repouso. Aplica-se ao bloco uma força de intensidade menor que o seu peso, numa direção que forma um ângulo q (0o ≤ θ ≤ 180o) com o eixo horizontal x. a) Qual a condição para que o bloco entre em movimento?
b) Sendo m a massa do corpo, obtenha a intensidade da aceleração do bloco em função de F, m e q.